第５章問題解決とその方法

４節シミュレーション

［第５章問題解決とその方法］

複利法による預金額（確定的モデル）

授業第５回

【課題】

銀行に１００,０００円を預けた。利率が年５％の複利であるとき，１０年後までの毎年の預金残高を表示したい。
※複利とは，利子が利子を生む仕組みのこと。
利子を受け取り，利子に利子がつかない仕組みは単利という。

【考察】

数式モデル
［利子］=［元金 or 前年の預金額］×［利率］
［初年度預金顎］=［元金］+［初年度の利子］
［以降の預金額］=［前年の預金額］+［前年度の利子］

変数一覧

元金
預金額
利率
利子
経過年

：gankin
：yokin
：riritsu
：rishi
：nen

【DNCL】

gankin = 100000
riritsu = 0.05

選択肢

yokin = gankin
nen を 0 から 10 まで 1 ずつ増やしながら繰り返す:
│   rishi = yokin * riritsu
│   表示する(nen,"年目：預金額",yokin,"円：利子",rishi,"円")
⎿   yokin = yokin + rishi

⇨ IDEで動作確認

gankin   rishi   gankin*rishi
gankin*riritsu   yokin*riritsu   rishi*riritsu
gankin+rishi   yokin+rishi   gankin+yokin

Python

［通常版］

gankin = 100000
riritsu = 0.05
yokin = gankin
for nen in range(11):
    rishi = yokin * riritsu
    print(nen,"年目：預金額",yokin,"円：利子",rishi,"円")
    yokin = yokin + rishi

［研究：グラフ表示版］ ※授業で用いたmonacaでは動作しません。

import matplotlib.pyplot as plt
gankin = 100000
riritsu = 0.05
yokin = gankin
x = [0]
y = [yokin]
for nen in range(11):
    rishi = yokin * riritsu
    print(nen,"年目：預金額",yokin,"円：利子",rishi,"円")
    yokin = yokin + rishi
    x.append(nen+1)
    y.append(yokin)
plt.plot(x,y)
plt.show()

放水による貯水池の水量（確定的モデル）

授業第６回 ※未実施

【課題】

最大貯水量15000㎥の本北方貯水池は次のように管理されている。
毎日，残りの貯水量に対して15%の割合に当たる量を放水する。
残りの貯水量が最大貯水量の20％以下となったとき放水を停止する。
さて，最初の貯水量が12000m³であるとき，今後30日間の貯水量が
どうなるか調べてみよう。

【考察】

数式モデル
［放水量］=［貯水量］×［放水割合］
［仮貯水量］=［前日の貯水量］ｰ［前日の放水量］
※放水停止量を下回った時点で放水は停止するが，停止しないものとして仮に算出しておく。
［貯水量］=［仮貯水量］と［放水停止量］の大きい方
※仮貯水量が放水停止量より多いときは仮貯水量，少ないときは放水停止量となる。

変数一覧

貯水量
最大貯水量
最初の貯水量
仮貯水量
放水量
放水割合
放水停止量
放水停止割合
経過日数
最大経過日数

：chosui
：chosuimax
：chosuistart
：chosuikari
：hosui
：hosuiwariai
：hosuiteishi
：hosuiteishiwariai
：day
：daymax

※日々変動する貯水量

※貯水量が放水停止量より少なくなっても
放水を停止せず，そのまま続けたときに
到達すると考えられる計算上の貯水量

※放水を停止するときの貯水量

※初日は｢0｣とする
※ここでは｢30｣である

アルゴリズムの工夫
放水量は，その時点での貯水量（前日の貯水量）から算出している。
ところが，放水中に貯水量が放水停止量を下回ったならば，本来はその時点で放水を停止しなくてはならない。従ってその日の放水量は先に計算をした放水量より少なくなる。
これを実現するため，放水停止量を下回っても気にせず，そのまま計算した仮貯水量という仮想的な数量を導入する。そしてもしその値が放水停止量以上ならば，そのまま仮貯水量を貯水量とし，放水量も計算どおりとする。逆にもし下回るようならば，貯水量は放水停止量とし，放水量は元の貯水量と放水停止量の差として求めることにした。

【DNCL】

chosuimax = 15000
chosuistart = 12000

選択肢

hosuiwariai = 0.15
hosuiteishiwariai = 0.20
daymax = 30

hosuiteishi = chosuimax * hosuiteishiwariai
chosui = chosuistart

day を 0 から daymax まで 1 ずつ増やしながら繰り返す:

│ hosui = chosui * hosuiwariai
│ chosuikari = chosui - hosui

│   もし chosuikari < hosuiteishi ならば:
│   ⎿   hosui = chosui - hosuiteishi
│   表示する(day,"日：貯水量",chosui,"：放水量",hosui)
⎿   chosui = chosui - hosui

⇨ IDEで動作確認

chosuimax*hosuiteishiwariai chosuisart*hosuiwariai chosuistart*hosuiteishiwariai chosui*hosuiwariai chosui+hosui chosui-hosui chosuikari-housui chosui+hosuiteishi chosui-hosuiteishi

Python

［通常版］

chosuimax = 15000
chosuistart = 12000
hosuiwariai = 0.15
hosuiteishiwariai = 0.20
daymax = 30

hosuiteishi = chosuimax * hosuiteishiwariai
chosui = chosuistart

for day in range(0,daymax+1):
    hosui = chosui * hosuiwariai
    chosuikari = chosui - hosui
    if chosuikari < hosuiteishi:
        hosui = chosui - hosuiteishi
    print(day,"日：貯水量",chosui,"：放水量",hosui)
    chosui = chosui - hosui

［研究：グラフ表示版］ ※授業で用いたmonacaでは動作しません。

import matplotlib.pyplot as plt 

chosuimax = 15000
chosuistart = 12000
hosuiwariai = 0.15
hosuiteishiwariai = 0.20
daymax = 30
x_day = []
y_chosui = []
y_hosui = []

hosuiteishi = chosuimax * hosuiteishiwariai
chosui = chosuistart

for day in range(0,daymax+1):
    hosui = chosui * hosuiwariai
    chosuikari = chosui - hosui
    if chosuikari < hosuiteishi:
        hosui = chosui - hosuiteishi
    print(day,"日：貯水量",chosui,"：放水量",hosui)
    x_day.append(day)
    y_chosui.append(chosui)
    y_hosui.append(hosui)
    chosui = chosui - hosui

plt.plot(x_day,y_chosui) 
plt.plot(x_day,y_hosui) 
plt.show()

焼きそば店のおつり（確率的モデル）

授業第７回

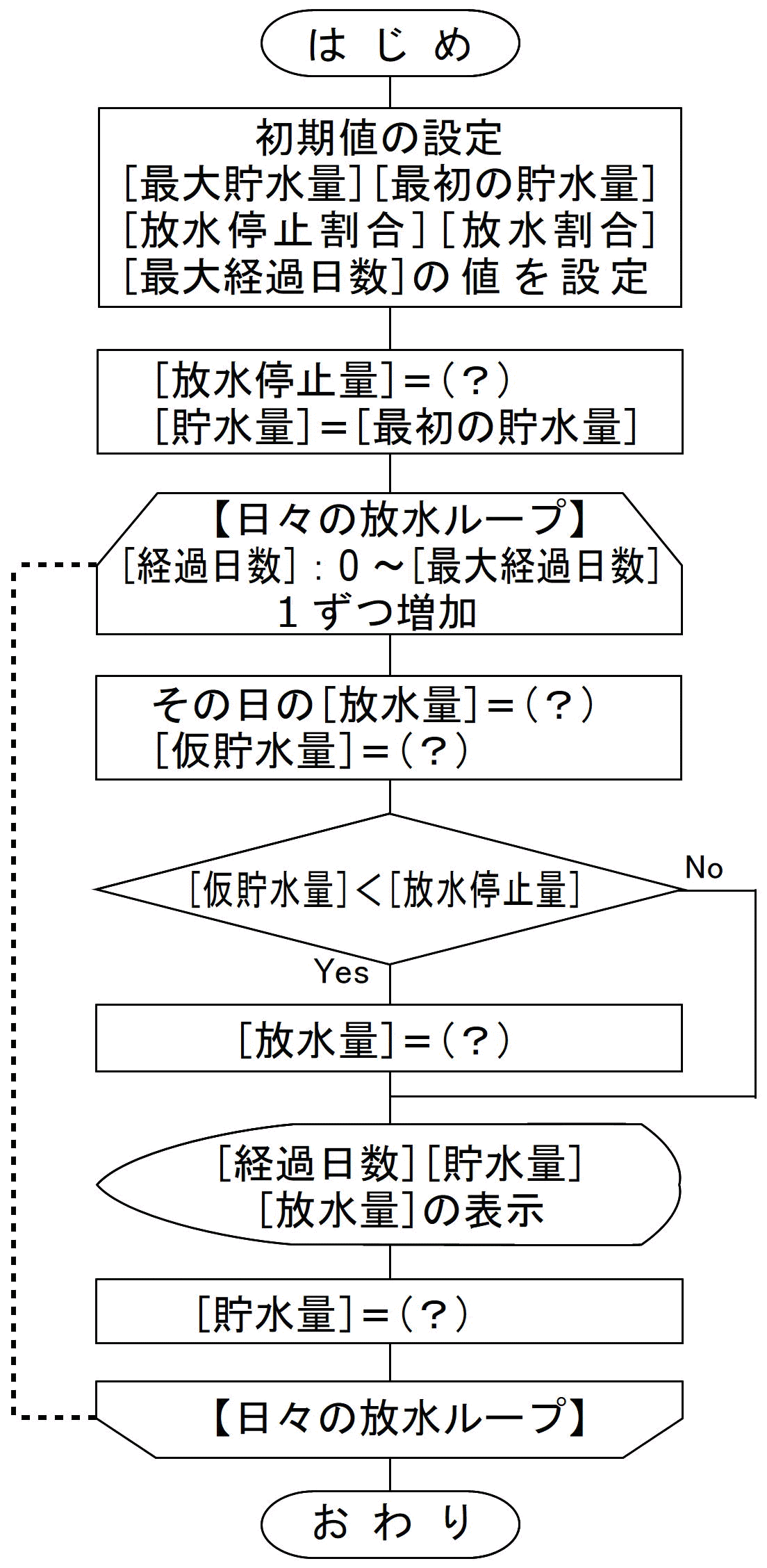
【課題】

一人一皿限定の200円，現金扱いのみの焼きそば店を開くことにした。
お客は料金を100円玉で支払うか，500円玉で支払いお釣りを100円玉で受け取るかのいずれかである。これまでの記録から，お客が100円玉で支払う確率は70%であることが分かっている。
全部で100皿を販売する計画を立てた。開店前にお釣り用の100円硬貨を何枚用意すればよいか，望ましい枚数を提案して欲しい。

【考察】

アルゴリズムの要点

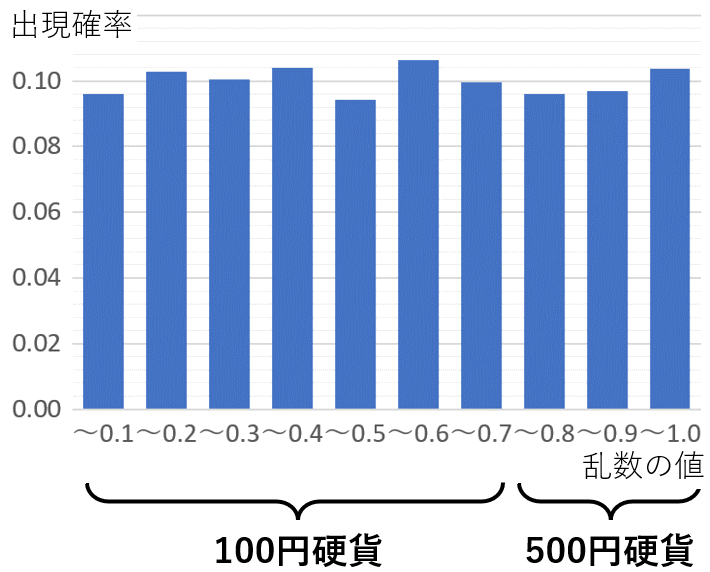
・それぞれのお客が100円硬貨で支払うか500円硬貨で支払うかは，
コンピュータで発生した 0 以上 1 未満の乱数の値により決める。
・支払いが100円硬貨のときは，100円硬貨が2枚増加する。また支払いが
500円硬貨のときは，500円硬貨が1枚増加し，100円硬貨が3枚減少する。
・100円硬貨の最小枚数は，毎回支払いが終わった時点で，そのときの枚数と
その前までの最小枚数とを比較し，より小さい方を以降の最小枚数とする。

変数一覧

販売総数
支払い硬貨の決定確率
100円硬貨の枚数
500円硬貨の枚数
100円硬貨の最小枚数
お客の番号（1～sosu）

：sosu
：kakuritsu
：coin100
：coin500
：min100
：kyaku

関数の説明

乱数() ･･･ 0 以上 1 未満のランダムな小数を返す。
例えば，x = 乱数() のとき x に 0.57309 など無作為な小数が代入される。

【DNCL】

sosu = 100
kakuritsu = 0.7

選択肢

coin100 = 0
coin500 = 0

min100 = 300
kyaku を 1 から sosu まで 1 ずつ増やしながら繰り返す:
│   もし乱数() < kakuritsu ならば:
│   │   coin100 = coin100 + 2
│   そうでなければ:

│ │ coin500 = coin500 + 1
│ │ coin100 = coin100 - 3

│   │   もし coin100 < min100 ならば:
│   ⎿   ⎿   min100 = coin100
⎿   表示する("客",kyaku,"：100円",coin100,"：500円",coin500)

表示する("100円硬貨最小枚数：",min100)

⇨ IDEで動作確認

coin100-1 coin100-3 coin100+2 coin100+1
coin500-1 coin500-3 coin500+2 coin500+1
coin100=min100 min100=coin100+coin500
min100=coin100 min100=coin100-coin500

【研究：配列を用いたDNCL】

すべてのお客について，支払い後の100円硬貨の枚数と500円硬貨の枚数を配列変数に代入していく手法でコーディングしてみよう。あるお客の支払後の各硬貨の枚数は，その前のお客の支払後の各硬貨の枚数を増減させたものになる。100円硬貨の枚数の最小値は，その最小値を与えるお客の番号を記録しておくこととする。

変数一覧

販売総数
支払い硬貨の決定確率
100円硬貨の枚数
500円硬貨の枚数
お客の番号（1～sosu）
枚数最小のお客番号

：sosu
：kakuritsu
：配列 Coin100
：配列 Coin500
：kyaku
：minkyaku

Coin100[0]，Coin500[0]
：初期値（開店前の硬貨枚数）
Coin100[n]，Coin500[n]
：n番目のお客の後の硬貨枚数
minkyaku：100円硬貨の
枚数を最小にするお客の番号

sosu = 100
kakuritsu = 0.7

選択肢

Coin100 の全ての値を0にする
Coin500 の全ての値を0にする

minkyaku = 0
Coin100[minkyaku] = 0 #開店前に準備した100円硬貨の枚数
kyaku を 1 から sosu まで 1 ずつ増やしながら繰り返す:
│ もし乱数() < kakuritsu ならば:

│ │ Coin100[kyaku] = Coin100[kyaku - 1] + 2
│ │ Coin500[kyaku] = Coin500[kyaku - 1]

│ そうでなければ:

│   │   Coin100[kyaku] = Coin100[kyaku - 1] - 3
│   │   Coin500[kyaku] = Coin500[kyaku - 1] + 1
│   │   もし Coin100[kyaku] < Coin100[minkyaku] ならば:

│   ⎿   ⎿   minkyaku = kyaku
│   表示する("客",kyaku,"：100円硬貨",Coin100[kyaku],
⎿    "：500円硬貨",Coin500[kyaku])
表示する("100円硬貨最小枚数：",Coin100[minkyaku])

⇨ IDEで動作確認

Coin100[kyaku-1]
Coin100[kyaku-1]+2
Coin100[kyaku+1]+1
Coin100[kyaku-1]-3
minkyaku=kyaku
Coin100[kyaku]

Coin500[kyaku-1]
Coin500[kyaku+1]-1
Coin500[kyaku-1]+2
Coin500[kyaku-1]+1
kyaku=minkyaku
Coin100[minkyaku]

Python

［通常版］

import random

sosu = 100
kakuritsu = 0.7
coin100 = 0
coin500 = 0

coin100min = 300
for kyaku in range(1,sosu+1):
    if random.random() < kakuritsu:
        coin100 = coin100 + 2
    else:
        coin500 = coin500 + 1
        coin100 = coin100 - 3
        if coin100 < coin100min:
            coin100min = coin100
    print("客",kyaku,"：100円硬貨",coin100,"：500円硬貨",coin500)

print("100円硬貨 最小枚数：",coin100min)

［研究：グラフ表示版］ ※授業で用いたmonacaでは動作しません。

import random
import matplotlib.pyplot as plt

sosu = 100
kakuritsu = 0.7
coin100 = 0
coin500 = 0

Kyaku = []
Coin100 = []
Coin500 = []

coin100min = 300
for kyaku in range(1,sosu+1):
    if random.random() < kakuritsu:
        coin100 = coin100 + 2
    else:
        coin500 = coin500 + 1
        coin100 = coin100 - 3
        if coin100 < coin100min:
            coin100min = coin100
    print("客",kyaku,"：100円硬貨",coin100,"：500円硬貨",coin500)

    Kyaku.append(kyaku)
    Coin100.append(coin100)
    Coin500.append(coin500)

print("100円硬貨 最小枚数：",coin100min)

plt.plot(Kyaku,Coin100)
plt.plot(Kyaku,Coin500)
plt.show()